Ray Marching là gì ?
Trong thế giới đồ họa máy tính, chúng ta đã quá quen thuộc với hai kỹ thuật dựng hình (rendering) phổ biến là Rasterization (được dùng trong hầu hết game) và Ray Tracing (mang lại chất lượng điện ảnh). Tuy nhiên, có một kỹ thuật khác cũng không kém phần mạnh mẽ và linh hoạt, đặc biệt hiệu quả với các hình khối phức tạp: đó chính là Ray Marching.
Vậy Ray Marching là gì và tại sao nó lại được coi là “phép thuật”? Hãy cùng tìm hiểu qua bài viết này.
Ray Marching vs. Ray Tracing: Khác Biệt Ở Đâu?
Để hiểu Ray Marching, trước tiên hãy nhắc lại một chút về “người anh em” Ray Tracing.
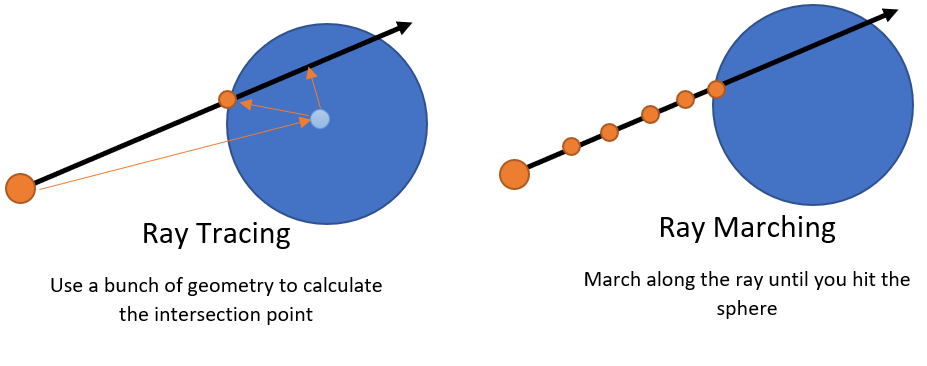
Với Ray Tracing, chúng ta bắn một tia sáng (ray) từ camera qua mỗi pixel trên màn hình và tính toán chính xác điểm giao cắt của tia đó với các vật thể trong cảnh. Việc này đòi hỏi các phương trình toán học phức tạp để tìm giao điểm.
Ray Marching cũng bắn một tia sáng, nhưng thay vì giải phương trình, nó “dò dẫm” từng bước một dọc theo tia đó để tìm bề mặt vật thể. Quá trình này giống như bạn đi trong một căn phòng tối, mỗi bước bạn sẽ vươn tay ra để xem có chạm vào tường không, và khoảng cách bạn có thể bước tiếp chính là khoảng cách an toàn ngắn nhất tới bức tường đó.
“Phép thuật” Đằng Sau Ray Marching: Signed Distance Function (SDF)
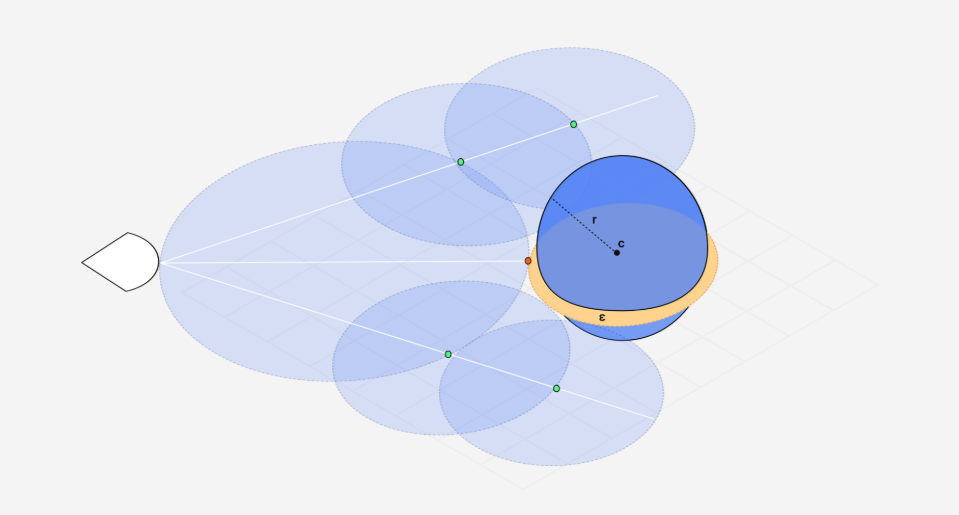
Làm thế nào Ray Marching biết được “bước đi” tiếp theo nên dài bao nhiêu? Bí mật nằm ở một khái niệm gọi là Signed Distance Function (SDF), hay Hàm khoảng cách có dấu.
SDF là một hàm nhận đầu vào là một điểm trong không gian 3D và trả về khoảng cách ngắn nhất từ điểm đó tới bề mặt của một vật thể.
- Nếu điểm đó nằm ngoài vật thể, SDF trả về một số dương.
- Nếu điểm đó nằm trong vật thể, SDF trả về một số âm.
- Nếu điểm đó nằm trên bề mặt vật thể, SDF trả về 0.
Giá trị mà SDF trả về chính là “bán kính an toàn”. Chúng ta có thể di chuyển điểm hiện tại dọc theo tia sáng một khoảng bằng đúng giá trị này mà không sợ bị “xuyên” qua vật thể.
Sơ Đồ Thuật Toán Ray Marching
Thuật toán Ray Marching hoạt động như một vòng lặp lặp đi lặp lại các bước dò dẫm. Dưới đây là sơ đồ chi tiết:
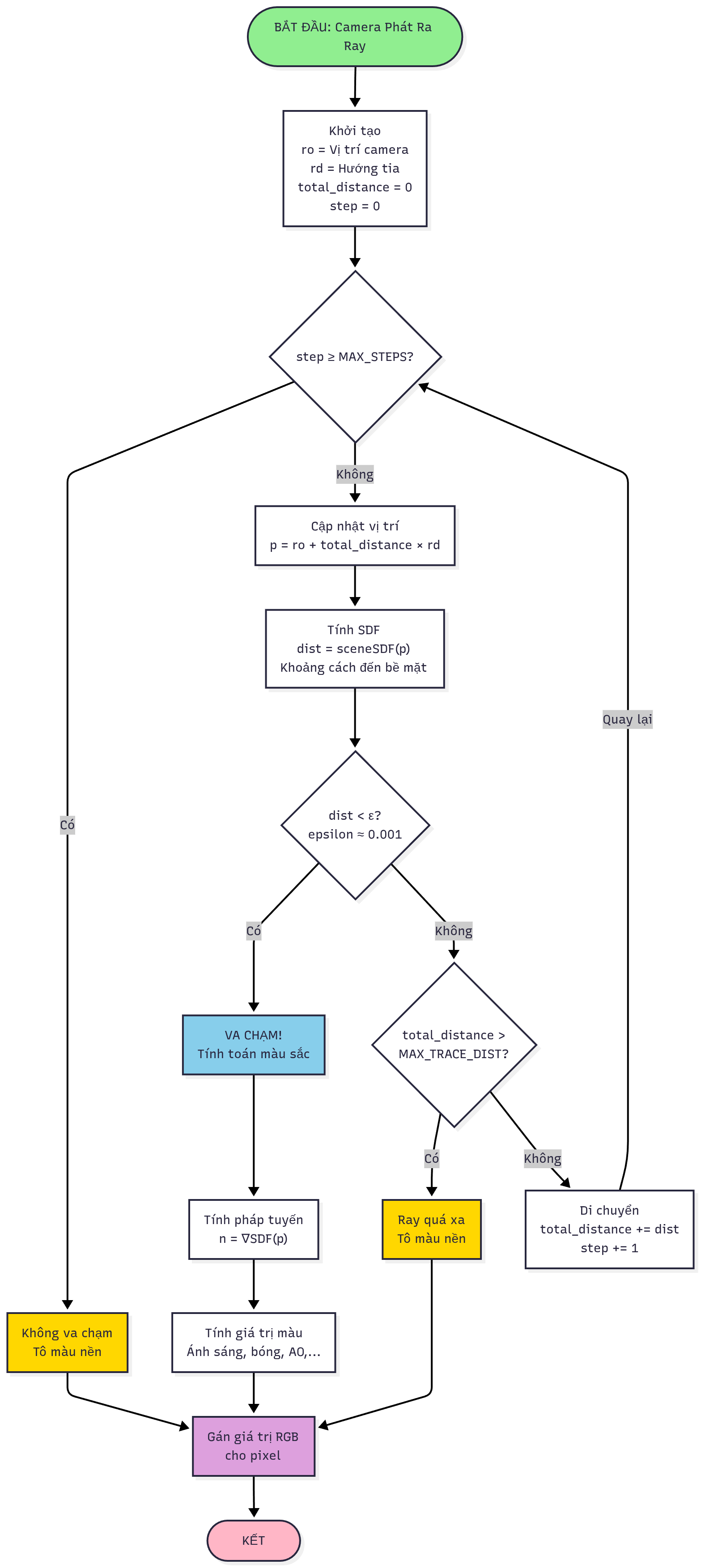
Giải Thích Chi Tiết Từng Bước
Bước 1: Khởi Tạo Tia Sáng
Quá trình bắt đầu khi camera phát ra một tia sáng hướng vào cảnh 3D. Mỗi pixel trên màn hình tương ứng với một tia sáng riêng.
- Vị trí bắt đầu (
ro– ray origin): Tọa độ của camera - Hướng tia (
rd– ray direction): Hướng từ camera tới pixel hiện tại (đã được chuẩn hóa) - Tổng khoảng cách (
total_distance): Khởi tạo bằng 0 - Số bước (
step): Bắt đầu từ 0
Bước 2: Vòng Lặp Chính – Kiểm Tra Điều Kiện
Trước tiên, kiểm tra xem ta có thể tiếp tục hay không:
- Nếu
số bước < MAX_STEPS: Tiếp tục vòng lặp - Nếu
số bước >= MAX_STEPS: Dừng lặp, coi như ray đi quá xa
Tại sao cần MAX_STEPS? Để tránh vòng lặp vô hạn trong trường hợp ray không bao giờ chạm vật thể.
Bước 3: Cập Nhật Vị Trí Hiện Tại Trên Tia
Tính vị trí điểm hiện tại mà chúng ta đang kiểm tra:
$$p = ro + \text{total_distance} \times rd$$
ro: Vị trí camera (điểm bắt đầu)rd: Hướng chuẩn hóa của tiatotal_distance: Tổng khoảng cách đã di chuyển cho đến bước này
Bước 4: Tính Khoảng Cách Đến Bề Mặt (SDF)
Tại vị trí hiện tại p, tính hàm SDF của cảnh:
$$dist = \text{sceneSDF}(p)$$
Giá trị dist trả về cho chúng ta biết:
- Nếu
dist > 0: Điểm hiện tại ở ngoài vật thể, khoảng cách đến bề mặt làdist - Nếu
dist < 0: Điểm hiện tại ở trong vật thể - Nếu
dist = 0: Điểm nằm trên bề mặt (hiếm khi xảy ra)
Bước 5: Kiểm Tra Va Chạm
So sánh dist với ngưỡng epsilon (thường là 0.001 hoặc 0.0001):
$$\text{if } dist < \varepsilon \text{ then COLLISION}$$
- Nếu
dist < epsilon: Coi như ray đã va vào bề mặt → Dừng vòng lặp, chuyển sang tính toán màu sắc - Nếu
dist >= epsilon: Ray chưa va vào → Tiếp tục
Tại sao dùng epsilon thay vì chính xác bằng 0? Vì tính toán số thực trên máy tính không thể hoàn toàn chính xác, nên ta dùng một ngưỡng nhỏ.
Bước 6: Kiểm Tra Ray Quá Xa
Nếu ray đã di chuyển quá xa mà vẫn chưa chạm vật thể:
$$\text{if } \text{total_distance} > \text{MAX_TRACE_DIST}$$
- Nếu đúng: Coi như ray đã “thoát ra khỏi không gian”, không có va chạm
- Nếu sai: Tiếp tục bước 7
Tại sao cần MAX_TRACE_DIST? Để tránh chi phí tính toán quá lớn cho những tia không bao giờ gặp vật thể.
Bước 7: Cập Nhật Khoảng Cách và Tiếp Tục
Nếu vẫn chưa va chạm và chưa quá xa, di chuyển con trỏ trên tia:
$$\text{total_distance} := \text{total_distance} + dist$$
Đây là “bước nhảy” đặc trưng của ray marching:
- Di chuyển một khoảng bằng chính giá trị SDF
- Lý do: SDF cho biết khoảng cách an toàn tối đa, nên ta có thể nhảy ngay tới đó mà không lo xuyên qua bề mặt
- Lợi ích: Giảm số bước cần thiết so với phương pháp nhảy cố định
Sau đó, tăng bộ đếm bước: step := step + 1 và quay lại Bước 2.
Bước 8: Xử Lý Kết Quả – Trường Hợp Va Chạm Thành Công
Khi vòng lặp kết thúc với điều kiện dist < epsilon, ta đã tìm được điểm va chạm. Bây giờ, cần tính toán giá trị màuđể gán vào pixel.
Bước 8.1: Tính Pháp Tuyến (Normal Vector)
Pháp tuyến là vector vuông góc với bề mặt tại điểm va chạm, rất quan trọng để tính ánh sáng.
$$\vec{n} = \text{normalize}(\nabla S(\vec{p}))$$
Chúng ta xấp xỉ gradient bằng sai phân hữu hạn:
$$\nabla S(\vec{p}) \approx \frac{1}{2\epsilon} \begin{pmatrix}
S(\vec{p} + \epsilon\hat{x}) – S(\vec{p} – \epsilon\hat{x}) \
S(\vec{p} + \epsilon\hat{y}) – S(\vec{p} – \epsilon\hat{y}) \
S(\vec{p} + \epsilon\hat{z}) – S(\vec{p} – \epsilon\hat{z})
\end{pmatrix}$$
Trong đó $\epsilon$ là một hằng số rất nhỏ (thường 0.001).
Ý nghĩa: Pháp tuyến cho biết hướng mà bề mặt “nhìn ra ngoài”. Nó được dùng để:
- Tính độ sáng của ánh sáng lan tỏa (diffuse lighting)
- Tính phản xạ (specular reflection)
- Xác định hướng bóng

Bước 8.2: Tính Toán Thành Phần Ánh Sáng
Màu sắc cuối cùng là kết hợp của nhiều thành phần ánh sáng:
A. Ánh Sáng Môi Trường (Ambient Light)
$$C_{\text{ambient}} = C_{\text{material}} \times I_{\text{ambient}}$$
- $C_{\text{material}}$: Màu cơ bản của vật thể
- $I_{\text{ambient}}$: Cường độ ánh sáng môi trường (thường là hằng số nhỏ, ví dụ 0.2)
Mục đích: Đảm bảo các khu vực không bị sáng trực tiếp vẫn có màu chứ không hoàn toàn đen.
B. Ánh Sáng Lan Tỏa (Diffuse Lighting)
$$C_{\text{diffuse}} = C_{\text{material}} \times I_{\text{light}} \times \max(0, \vec{n} \cdot \vec{l})$$
Trong đó:
- $\vec{l}$: Vector từ điểm va chạm tới nguồn sáng (chuẩn hóa)
- $\vec{n} \cdot \vec{l}$: Tích vô hướng giữa pháp tuyến và hướng sáng
- $\max(0, \cdots)$: Đảm bảo giá trị không âm (bề mặt hướng về phía sau sáng sẽ không được sáng)
Ý nghĩa công thức:
- Khi pháp tuyến song song với hướng sáng ($\vec{n} \cdot \vec{l} = 1$): Bề mặt được sáng tối đa
- Khi pháp tuyến vuông góc với hướng sáng ($\vec{n} \cdot \vec{l} = 0$): Bề mặt không được sáng
- Khi pháp tuyến hướng về phía đối diện ($\vec{n} \cdot \vec{l} < 0$): Bề mặt nằm trong bóng
C. Ánh Sáng Phản Chiếu (Specular Lighting)
$$C_{\text{specular}} = I_{\text{light}} \times \max(0, \vec{r} \cdot \vec{v})^{\alpha}$$
Trong đó:
- $\vec{r}$: Vector phản chiếu của sáng trên bề mặt
- $\vec{v}$: Vector từ điểm va chạm tới camera
- $\alpha$: Tham số độ bóng của vật liệu (shininess). Giá trị càng lớn, phản chiếu càng sắc nét
Ý nghĩa: Tạo những đốm sáng bóng (highlight) trên bề mặt, làm cho vật thể trông bóng bẩy hơn.
D. Ambient Occlusion (AO)
$$AO = 1 – \sum_{i=0}^{n} \frac{\max(0, \text{SDF}(p + i \times d \times \delta) – d)}{d \times (i+1)}$$
Trong đó:
- $d$: Khoảng cách lấy mẫu
- $\delta$: Hệ số tăng khoảng cách
- $n$: Số lần lấy mẫu
Ý nghĩa: Tính bóng nhạt tự nhiên trong các nếp gấp và góc của vật thể, làm cho chúng trông sâu hơn.
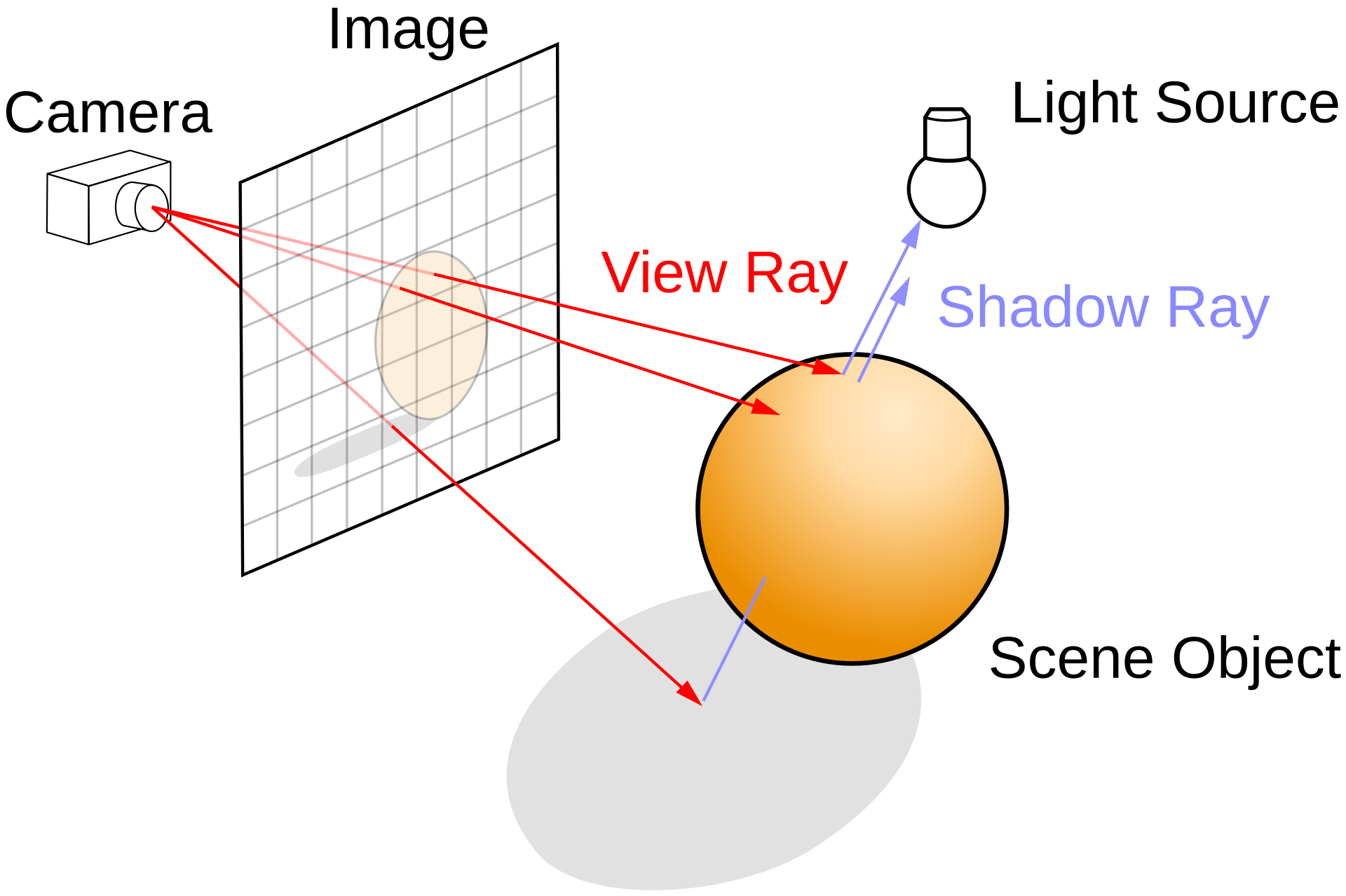
E. Bóng Mềm (Soft Shadow)
$$\text{shadow} = \min(1, k \times \frac{\text{SDF}(p + \vec{l} \times t)}{t})$$
Lấy mẫu SDF dọc theo hướng sáng để xác định xem điểm hiện tại có bị che bóng bởi vật thể khác không.
Ý nghĩa: Tạo các bóng mềm mại thay vì bóng cứng, trông tự nhiên hơn.
Bước 8.3: Kết Hợp Các Thành Phần
Màu sắc cuối cùng được tính bằng:
$$C_{\text{final}} = C_{\text{ambient}} + (C_{\text{diffuse}} + C_{\text{specular}}) \times \text{shadow} \times AO$$
Hoặc trong trường hợp đơn giản hơn:
$$C_{\text{final}} = C_{\text{ambient}} + C_{\text{diffuse}} \times \text{shadow}$$
Bước 8.4: Gán Giá Trị RGB Cho Pixel
Sau khi tính toán được giá trị màu cuối cùng $C_{\text{final}} = (R, G, B)$, ta gán nó vào pixel hiện tại trên màn hình:
$$\text{frameBuffer}[\text{pixelX}, \text{pixelY}] = C_{\text{final}}$$
Hoặc nếu cần chuyển đổi từ khoảng [0, 1] sang [0, 255]:
$$\text{pixelColor} = \lfloor C_{\text{final}} \times 255 \rfloor$$
Quá trình hoàn tất: Pixel này giờ đã có màu sắc phù hợp, phản ánh ánh sáng, bóng, và các tính chất bề mặt của vật thể.

Ví Dụ Minh Họa Thực Tế – Tính Toán Màu Chi Tiết
Hãy xem một ví dụ cụ thể về cách tính toán màu khi va chạm thành công:
Giả sử ta có:
- Điểm va chạm: $p = (0, 0, 1)$ (trên bề mặt hình cầu)
- Pháp tuyến tại điểm đó: $\vec{n} = (0, 0, 1)$ (hướng lên)
- Vị trí nguồn sáng: $L = (1, 1, 2)$
- Vị trí camera: $C = (0, 0, -5)$
- Màu vật thể: $C_{\text{material}} = (1.0, 0.5, 0.2)$ (màu cam)
- Cường độ ánh sáng: $I_{\text{light}} = 1.0$
Tính toán từng bước:
- Vector hướng sáng (chuẩn hóa):
$$\vec{l} = \text{normalize}(L – p) = \text{normalize}((1, 1, 1)) = (0.577, 0.577, 0.577)$$ - Tích vô hướng:
$$\vec{n} \cdot \vec{l} = (0, 0, 1) \cdot (0.577, 0.577, 0.577) = 0.577$$ - Ánh sáng môi trường:
$$C_{\text{ambient}} = (1.0, 0.5, 0.2) \times 0.2 = (0.2, 0.1, 0.04)$$ - Ánh sáng lan tỏa:
$$C_{\text{diffuse}} = (1.0, 0.5, 0.2) \times 1.0 \times 0.577 = (0.577, 0.289, 0.115)$$ - Kiểm tra bóng (giả sử không bị che bóng):
$$\text{shadow} = 1.0$$ - Màu sắc cuối cùng:
$$C_{\text{final}} = (0.2, 0.1, 0.04) + (0.577, 0.289, 0.115) \times 1.0$$
$$= (0.777, 0.389, 0.155)$$ - Chuyển đổi sang RGB 0-255:
$$\text{pixelColor} = (198, 99, 39)$$
Kết quả: Pixel này sẽ hiển thị màu cam nâu, với bóng tự nhiên giống một hình cầu được sáng từ phía trên.
Các Công Thức SDF Cơ Bản
Vậy hàm sceneSDF được xây dựng như thế nào? Nó dựa trên các hàm SDF của các hình khối cơ bản và các phép toán để kết hợp chúng lại.
1. SDF Của Các Hình Khối Cơ Bản (Primitives)
Hình Cầu (Sphere)
Cho điểm $\vec{p}$ trong không gian, tâm cầu tại $\vec{c}$, bán kính $r$:
$$\text{SDF}_{\text{sphere}}(\vec{p}, \vec{c}, r) = ||\vec{p} – \vec{c}|| – r$$
Ý nghĩa: Tính khoảng cách từ điểm đến tâm cầu, rồi trừ bán kính. Nếu kết quả dương, điểm nằm ngoài; âm, điểm nằm trong.
Hình Hộp (Box)
Cho điểm $\vec{p}$, tâm hộp tại $\vec{c}$, và nửa kích thước $\vec{b} = (b_x, b_y, b_z)$:
$$\begin{align}
\vec{q} &= |\vec{p} – \vec{c}| – \vec{b} \
\text{SDF}{\text{box}}(\vec{p}, \vec{c}, \vec{b}) &= ||\max(\vec{q}, \vec{0})|| + \min(\max(qx, q_y, q_z), 0)
\end{align}$$
Ý nghĩa: Công thức này tính khoảng cách đến cạnh hoặc bề mặt gần nhất của hộp.
Hình Trụ (Cylinder)
Cho điểm $\vec{p}$, trục trụ dọc theo trục $z$, bán kính $r$, chiều cao $h$:
$$\text{SDF}{\text{cylinder}}(\vec{p}, r, h) = \sqrt{(p_x^2 + py^2 – r)^2 + \max(|p_z| – h/2, 0)^2}$$
2. Kết Hợp Các Hình Khối (Boolean Operations)
Chúng ta có thể tạo ra các vật thể phức tạp bằng cách kết hợp khoảng cách $d_1$ (từ SDF của vật thể A) và $d_2$ (từ SDF của vật thể B):
Hợp (Union): Lấy hình dạng bao ngoài của hai vật thể.
$$\text{SDF}{\text{union}}(d_1, d_2) = \min(d1, d_2)$$
Giao (Intersection): Lấy phần chung của hai vật thể.
$$\text{SDF}{\text{intersection}}(d_1, d2) = \max(d_1, d_2)$$
Hiệu (Subtraction): “Đục” vật thể A bằng vật thể B.
$$\text{SDF}{\text{subtraction}}(d_1, d2) = \max(d_1, -d_2)$$
Ví dụ: Để tạo một hình cầu với một lỗ hình hộp bên trong:
$$\text{SDF}{\text{result}} = \text{max}(\text{SDF}{\text{sphere}}, -\text{SDF}_{\text{box}})$$
Ưu Điểm và Nhược Điểm
Ưu Điểm
- Dựng Hình Các Khối Phức Tạp: Cực kỳ mạnh mẽ để vẽ các hình dạng không có biểu diễn đa giác rõ ràng như fractals, metaballs, hoặc các bề mặt được tạo ra từ thuật toán (procedural geometry).
- Không Cần Bộ Nhớ Lớn: Không cần lưu trữ một lượng lớn các đỉnh và tam giác như đồ họa 3D truyền thống. Chỉ cần các hàm toán học mô tả hình dạng.
- Hiệu Ứng Đẹp Mắt: Dễ dàng tính toán các hiệu ứng như đổ bóng mềm (soft shadows) và ambient occlusion với độ chính xác cao.
- Biến Đổi Động: Thay đổi hình dạng vật thể chỉ bằng cách thay đổi hàm SDF, phù hợp cho hiệu ứng biến dạng (morphing).
Nhược Điểm
- Khó Biểu Diễn Các Chi Tiết Sắc Nét: Cạnh của vật thể có thể không sắc nét bằng Ray Tracing vì bản chất “dò dẫm” của thuật toán. Khoảng cách giao điểm phụ thuộc vào epsilon.
- Hiệu Năng: Có thể chậm hơn Rasterization đối với các cảnh đơn giản vì phải lặp nhiều lần. Tuy nhiên, với GPU hiện đại, có thể song song hóa tốt.
- Phụ Thuộc Vào SDF: Mọi vật thể trong cảnh đều phải có một hàm SDF tương ứng, việc này không phải lúc nào cũng dễ dàng. Đặc biệt khó với các mô hình mesh phức tạp.
- Hiệu Chỉnh Khó: Cần tinh chỉnh các tham số như MAX_STEPS, epsilon, MAX_TRACE_DIST để đạt được chất lượng tốt.
Kết Luận
Ray Marching là một kỹ thuật dựng hình độc đáo và mạnh mẽ, mở ra một thế giới hoàn toàn mới cho đồ họa máy tính, đặc biệt là trong lĩnh vực real-time graphics và demoscene. Mặc dù có những hạn chế riêng, sự linh hoạt và khả năng tạo ra những hình ảnh siêu thực từ các công thức toán học đơn giản đã khiến nó trở thành một công cụ không thể thiếu trong kho tàng của các lập trình viên đồ họa.
Với sự phát triển của GPU và các công cụ shader hiện đại, Ray Marching tiếp tục chứng minh giá trị của nó trong cộng đồng đồ họa, từ các tác phẩm nghệ thuật số trên Shadertoy cho đến các trò chơi độc lập sáng tạo.